函数核算的成果是正确的。关于 $ n = 5 $,其阶乘 $ 5! $ 等于 120。
Python求n的阶乘:办法与示例
阶乘是数学中的一个基本概念,用于描绘一个正整数与其一切正整数乘积的成果。在Python编程中,核算阶乘是一个常见的操练,能够协助咱们了解循环、递归以及函数等编程概念。本文将具体介绍Python中核算阶乘的几种办法,并供给相应的示例代码。
阶乘的界说

在数学中,一个正整数n的阶乘,记作n!,界说为从1乘到n的一切正整数的乘积。例如,5的阶乘(5!)等于5 × 4 × 3 × 2 × 1,成果为120。
运用循环核算阶乘
循环办法简介
运用循环核算阶乘是一种直观且易于了解的办法。以下是一个运用for循环核算阶乘的示例:
```python
def factorial_by_loop(n):
result = 1
for i in range(1, n 1):
result = i
return result
示例
n = 5
print(factorial_by_loop(n)) 输出:120
循环办法简介
运用循环核算阶乘是一种直观且易于了解的办法。以下是一个运用for循环核算阶乘的示例:
运用递归核算阶乘
递归办法简介
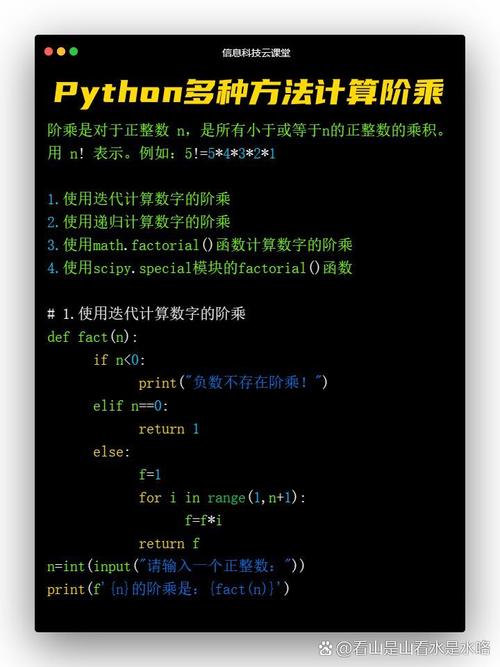
递归是一种函数调用本身的办法,用于处理能够分解为类似子问题的问题。以下是一个运用递归核算阶乘的示例:
```python
def factorial_by_recursion(n):
if n == 0 or n == 1:
return 1
else:
return n factorial_by_recursion(n - 1)
示例
n = 5
print(factorial_by_recursion(n)) 输出:120
递归办法简介

递归是一种函数调用本身的办法,用于处理能够分解为类似子问题的问题。以下是一个运用递归核算阶乘的示例:
运用math模块核算阶乘
math模块简介
Python的math模块供给了一个内置的阶乘函数,能够直接运用。以下是一个运用math模块核算阶乘的示例:
```python
import math
n = 5
print(math.factorial(n)) 输出:120
math模块简介
Python的math模块供给了一个内置的阶乘函数,能够直接运用。以下是一个运用math模块核算阶乘的示例:
高精度核算阶乘
高精度核算简介
当核算较大数的阶乘时,一般的整数类型或许无法包容成果。在这种情况下,能够运用高精度核算办法。以下是一个运用数组完成高精度核算阶乘的示例:
```python
def factorial_high_precision(n):
result = [1] 初始化成果数组
for i in range(2, n 1):
carry = 0 进位
for j in range(len(result)):
product = result[j] i carry
result[j] = product % 10 存储当时位
carry = product // 10 核算进位
while carry:
result.append(carry % 10)
carry //= 10
return result[::-1] 回转数组得到终究成果
示例
n = 100
print(''.join(map(str, factorial_high_precision(n)))) 输出:93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
高精度核算简介
当核算较大数的阶乘时,一般的整数类型或许无法包容成果。在这种情况下,能够运用高精度核算办法。以下是一个运用数组完成高精度核算阶乘的示例:
本文介绍了Python中核算阶乘的几种办法,包含循环、递归、运用math模块以及高精度核算。这些办法各有优缺点,适用于不同的场景。经过学习和实践这些办法,咱们能够更好地了解Python编程中的基本概念和技巧。